L'utilisation des résistances est très courante. Dans n'importe quel appareil électronique, quelle que soit le type, on a de fortes chances d'en trouver une.
Sommaire
C'est quoi une résistance électrique?
Une résistance électrique est un composant capable de s'opposer au passage du courant électrique qui circule dans un circuit électrique.
Symbole
 ou
ou 
Tous les matériaux ont une résistance plus ou moins élevée au passage d'un courant électrique. Ils sont classés comme conducteurs quand ils ont une faible résistance (or, cuivre, argent, aluminium), ou isolants quand ils ont une résistance élevée (papier, verre, caoutchouc, plastique, bois).
La résistance électrique est mesurée en Ohms, du nom du physicien Allemand Georg Simon Ohm (1784 - 1854), qui a étudié la relation entre la tension, le courant et la résistance, et, a découvert une loi qui porte son nom: la loi d'Ohm.
Loi d'Ohm
La différence de potentiel U entre les extrémités d'un conducteur ne fournissant que de l'énergie calorifique est égale au produit de la résistance R de ce conducteur par l'intensité du courant I qui le traverse:
\[\mathsf{U = RI}\]
Soit
\[\mathsf{R = \frac{U}{I}}\]
R: résistance (ou résistor) en Ohms (Ω).
I: courant en Ampères (A).
U: différence de potentiel en Volts (V).
Associations des résistances
Montage en série:
La résistance équivanlente
\[\mathsf{R_{eq} = R_1 + R_2 +...+ R_n}\]
Montage en parallèle:
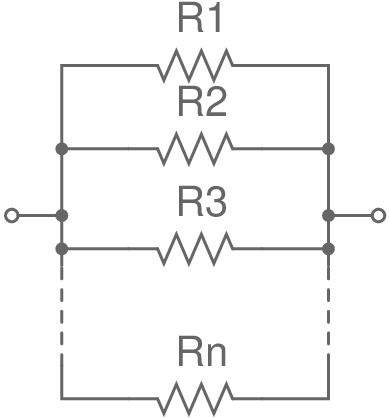
La résistance équivalente
\[\mathsf{\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_n}}\]
Autres types de montages:
Montage en pont
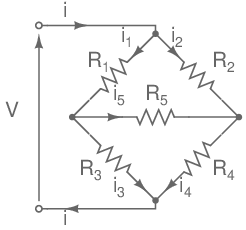
Ce montage est appelée pont de Wheatstone, du nom du physicien Anglais qui l'a amélioré et popularisé, Sir Charles Wheatstone (1803 - 1875).
Le courant i5 qui circule à travers la résistance R5 est donnée par:
Débranchons R5, puis appliquons le théorème de Thévénin entre les bornes C et D du pont:

Calcul de la tension à vide ETH:
i1 = i3 et i2 = i4; donc on peut appliquer la formule du pont diviseur de tension pour calculer VC le potentiel au point C et VD le potentiel au point D.
\[\mathsf{V_C=\frac{R_3}{R_1+R_3}.V}\]
\[\mathsf{V_D=\frac{R_4}{R_2+R_4}.V}\]
Le générateur de Thévénin
\[\mathsf{E_{TH}=V_C-V_D=\frac{R_3}{R_1+R_3}.V-\frac{R_4}{R_2+R_4}.V}\]
\[\mathsf{E_{TH}=\frac{R_3(R_2+R_4)-R_4(R_1+R_3)}{(R_1+R_3)(R_2+R_4)}.V=\frac{(R_2R_3-R_1R_4)}{(R_1+R_3)(R_2+R_4)}.V}\]
Calcul de la résistance RTH, lorsque V est court-circuité (= 0):
Le pont équivaut au schéma ci-après:
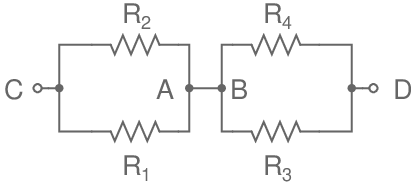
Donc RTH équivaut à (R2//R1) en série avec (R4//R3)
\[\mathsf{=\frac{R_1R_3}{R_1+R_3}+\frac{R_2R_4}{R_2+R_4}}\]
\[\mathsf{R_{TH}=\frac{R_1R_3(R_2+R_4)+R_2R_4(R_1+R_3)}{(R_1+R_3)(R_2+R_4)}}\]
Le circuit équivalent du pont avec R5 branché permet de calculer aisément i5:
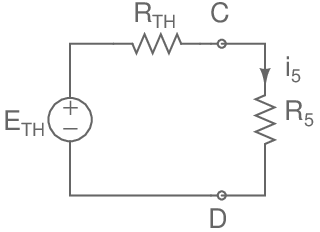
Avec les valeurs de RTH et ETH calculées précédemment, après simplification, on a
\[\mathsf{i_5=\frac{R_2R_3-R_1R_4}{R_5(R_1+R_3)(R_2+R_4)+R_1R_3(R_2+R_4)+R_2R_4(R_1+R_3)}.V}\]
On dit que le pont est équilibré lorsque le courant i5 = 0, soit:
\[\bbox[5px,border:1px solid]{\mathsf{R_2R_3=R_1R_4}}\]
Ce montage peut être utilisé pour déterminer la valeur d'une résistance inconnue.
Montage en étoile et en triangle
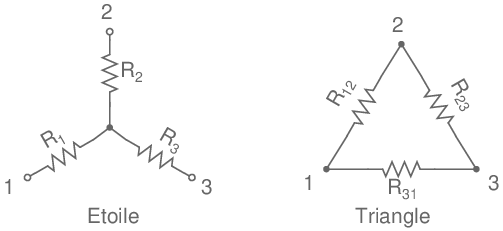
Il est possible de convertir l'étoile en triangle ou le triangle en étoile.
Pour une transformation Triangle - Etoile, il suffit de poser:
\[\bbox[5px,border:1px solid]{\mathsf{R_1=\frac{R_{12}R_{31}}{R_{12}+R_{23}+R_{31}}}}\]
\[\bbox[5px,border:1px solid]{\mathsf{R_2=\frac{R_{12}R_{23}}{R_{12}+R_{23}+R_{31}}}}\]
\[\bbox[5px,border:1px solid]{\mathsf{R_3=\frac{R_{23}R_{31}}{R_{12}+R_{23}+R_{31}}}}\]
Réciproquement, pour une transformation Etoile - Triangle on posera:
\[\bbox[5px,border:1px solid]{\mathsf{R_{12}=R_1+R_2+\frac{R_1R_2}{R_3}}}\]
\[\bbox[5px,border:1px solid]{\mathsf{R_{23}=R_2+R_3+\frac{R_2R_3}{R_1}}}\]
\[\bbox[5px,border:1px solid]{\mathsf{R_{31}=R_1+R_3+\frac{R_1R_3}{R_2}}}\]
Avec ce type de montage, on peut passer d'une structure en T vers une structure en ∏ et vice-versa.
Cas d'un matériau conducteur:
Tout matériau conducteur présente une résistance qui peut être calculée par la formule suivante:
\[\mathsf{R = ρ.\frac{\ell}{S}}\]
R : résistance en ohms.
\(\ell\) : longueur en mètres(m).
ρ : résistivité en ohms•mètres (Ω•m).
Comportement en température:
La résistivité varie en fonction de la température: ρ = ρ0(1 + α.θ).
ρ : résistivité en ohms.mètres.
ρ0 : résistivité pour θ = 0°C; en ohms.mètres.
α : coefficient de température (°C-1).
θ : température en degrés celcius (°C).
La résistance varie en fonction de la température: R = R0(1 + α•θ).
R : résistance à θ °C, en ohms.
R0 : résistance à 0 °C, en ohms.
α : coefficient de température en ppm/°C. (On l'appellera par la suite TCR).
θ : temprérature en degrés celcius.
Mesure d'une résistance:
Pour mesurer une résistance on peut utiliser soit un Ohmmètre, soit un multimètre en position Ohm. Ou alors un Ampèremètre et un Voltmètre puis appliquer la loi d'Ohm sur les deux lectures.

