Montages de bases à amplificateur opérationnel - régime linéaire:
Le fonctionnement en régime linéaire, impose que la sortie soit rebouclée sur l'entrée e- par l'intermédiaire d'un composant ou directement.
Pour les calculs sur tous les montages qui suivent, l' amplificateur opérationnel sera supposé idéal.
Montage inverseur:
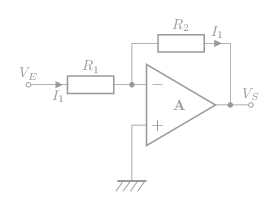
L'amplification:
\[\bbox[5px,border:1px solid]{\mathsf{{A_O =-\frac{V_S}{V_E}=-\frac{R_2}{R_1}}}}\]
Ampli op idéal: I+ = I- = 0 et ε = 0.
\[\mathsf{V_E= R_1I_1 \;et\; V_S = -R_2I_1}\]
\[\mathsf{A_O =-\frac{V_S}{V_E}=-\frac{R_2}{R_1}}\]
Montage non inverseur:
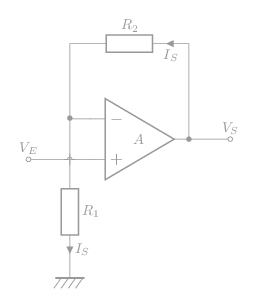
L'amplification:
\[\bbox[5px,border:1px solid]{\mathsf{A_O=\frac{V_S}{V_E}=\left(1+\frac{R_2}{R_1}\right)}}\]
Ampli op idéal:
\[\mathsf{V_E = V_{e+}=V_{e-}}\]
On peut déterminer Ve- avec la méthode du pont diviseur de tension:
\[\mathsf{V_E=V_{e-}=\frac{R_1}{R_1+R_2}V_S}\]
\[\mathsf{A_O=\frac{V_S}{V_E}=\left(1+\frac{R_2}{R_1}\right)}\]
Montage sommateur - inverseur:
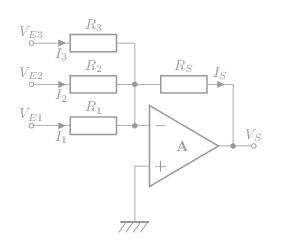
La tension de sortie:
\[\bbox[5px, border:1px solid]{\mathsf{V_S=-\frac{R_S}{R}(V_1+V_2+V_3)}}\]
Ampli op idéal: ε = 0;
Pour les courants:
\[\mathsf{I_1+I_2+I_3 = I_S}\tag{1}\label{1}\]
Les tensions:
\[\mathsf{V_1=R_1I_1; \;\; V_2=R_2I_2; \;\; V_3=R_3I_3\;et\;V_S=-R_SI_S}\]
Donc:
\[\mathsf{I_1=\frac{V_1}{R_1};\;\;I_2=\frac{V_2}{R_2};\;\;I_3=\frac{V_3}{R_3};\;et\;I_S=-\frac{V_S}{R_S}}\]
En substituant dans l' expression (1):
\[\mathsf{\frac{V_1}{R_1}+\frac{V_2}{R_2}+\frac{V_3}{R_3}=-\frac{V_S}{R_S}}\]
\[\mathsf{V_S=-R_S\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}+\frac{V_3}{R_3}\right)}\]
Supposons que R1 = R2 = R3 =R; on a:
\[\mathsf{V_S=-\frac{R_S}{R}(V_1+V_2+V_3)}\]
La tension de sortie est égale à la somme des tensions d'entrées.
Pour N entrées: l'équation 3-5 peut prendre cette forme générale:
\[\mathsf{V_S=-R_S\left(\frac{V_1}{R_1}+\frac{V_2}{R_2}+\cdots+\frac{V_N}{R_N}\right)}\]
Montage soustracteur:
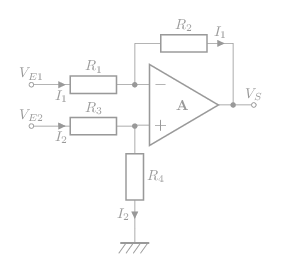
La tension de sortie:
\[\bbox[5px,border:1px solid]{\mathsf{V_S=V_{S2}+V_{S1}=\frac{R_4(R_1+R_2)}{(R_3+R_4)R_1}V_{E2}-\frac{R_2}{R_1}V_{E1}}}\]
On peut calculer la tension de sortie VS avec le théorème de superposition:
VE1 = 0, le montage devient:
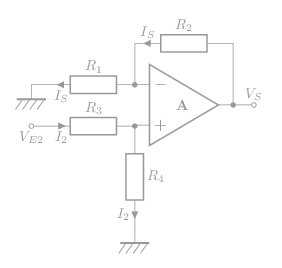
\[\mathsf{V_{e-}=\frac{R_1}{R_1+R_2}V_{S2}}\]
\[\mathsf{V_{e+}=\frac{R_4}{R_3+R_4}V_{E2}}\]
L'ampli op idéal: ε = 0 \(\implies\) Ve+= Ve-:
\[\mathsf{\frac{R_4}{R_3+R_4}V_{E2}=\frac{R_1}{R_1+R_2}V_{S2}}\]
\[\mathsf{V_{S2}=\frac{R_4(R_1+R_2)}{(R_3+R_4)R_1}V_{E2}}\tag{2-1}\label{2-1}\]
VE2 = 0, le montage devient:
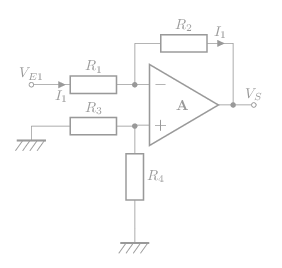
Les résistances R3 et R4 en parallèle n'ont aucune influence pour les calculs. Le montage équivaut à un inverseur déjà vu dans les lignes précédentes:
\[\mathsf{V_{S1}=-\frac{R_2}{R_1}V_{E1}}\tag{2-2}\label{2-2}\]
Pour finir la tension de sortie globale à partir des expressions (2-1) et (2-2)):
\[\mathsf{V_S=V_{S2}+V_{S1}=\frac{R_4(R_1+R_2)}{(R_3+R_4)R_1}V_{E2}-\frac{R_2}{R_1}V_{E1}}\tag{2-3}\label{2-3}\]
Si l'on pose: R1 = R3 et R2 = R4
La formule 2-3 devient:
\[\mathsf{V_S=\frac{R_2}{R_1}(V_{E2} - V_{E1})}\]
Montage suiveur:
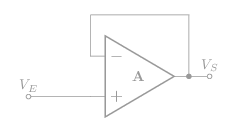
Ampli op idéal: \(\epsilon\)=0, \(\implies\) Ve+ = Ve-
\[\mathsf{V_S=V_{e-}\;et\; V_E =V_{e+}}\]
Donc:
\[\mathsf{V_S=V_E}\]
Amplificateur à gain élevé:
Dans certains cas, on a besoin d'obtenir un gain élevé, avec un montage inverseur ou non inverseur, même lorsque la valeur de la résistance de rebouclage R2 n'est pas très grande.
Montage 1: ampli inverseur:
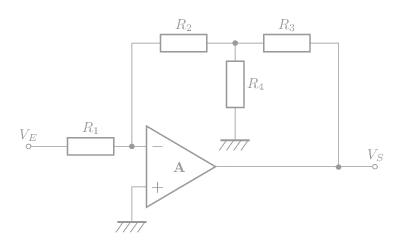
L'amplification:
\[\bbox[5px, border:1px solid]{\mathsf{\frac{V_S}{V_E}=-\frac{R_2}{R_1}\left(1+\frac{R_3}{R_2}+\frac{R_3}{R_4}\right)}}\]
L'amplification peut être calculée de deux manières différentes:
En utilisant les lois de Kirchoff:

Le courant qui circule à travers la résistance R1 est égal à celui qui circule à travers la résistance R2.
L'ampli op étant idéal, on peut écrire:
\[\mathsf{\frac{V_E}{R_1}=-\frac{V_M}{R_2}\;\implies\;V_M=-\frac{R_2}{R_1}V_E}\tag{3-1}\label{3-1}\]
Loi des courants:
\[\mathsf{I_3 = I_2+I_S}\]
Cela se traduit par:
\[\mathsf{\frac{V_M}{R_4}=\frac{(V_S-V_M)}{R_3}-\frac{V_M}{R_2}}\]
En regroupant tous les termes contenant VM, on obtient:
\[\mathsf{V_M\left(\frac{1}{R_4}+\frac{1}{R_2}+\frac{1}{R_3}\right)=\frac{V_S}{R_3}}\]
\[\mathsf{\implies\;V_S=\left(1+\frac{R_3}{R_2}+\frac{R_3}{R_4}\right)V_M}\tag{3-2}\label{3-2}\]
Si la formule 3-1 est substituée dans 3-2, on a:
\[\mathsf{V_S=-\frac{R_2}{R_1}\left(1+\frac{R_3}{R_2}+\frac{R_3}{R_4} \right)V_E}\]
L'amplification:
\[\mathsf{\frac{V_S}{V_E}=-\frac{R_2}{R_1}\left(1+\frac{R_3}{R_2}+\frac{R_3}{R_4} \right)}\]
Ce calcul peut aussi se faire en utilisant le théorème de Thévénin.
A droite du point A:

\[\mathsf{E_{Th}=\frac{R_4}{(R_3+R_4)}V_S\;et\;R_{Th}=\frac{R_3R_4}{(R_3+R_4)}}\]
Le schéma équivalent pourra ressembler à ceci:
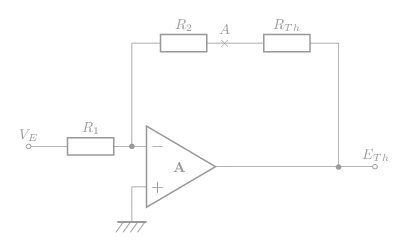
On peut écrire:
\[\mathsf{E_{Th}=-\left(\frac{R_2+R_{Th}}{R_1}\right)V_E=-\frac{R_2}{R_1}\left(1+\frac{R_{Th}}{R_2}\right)V_E}\]
soit:
\[\mathsf{\left(\frac{R_4}{R_3+R_4}\right)V_S=-\frac{R_2}{R_1}\left(1+\frac{R_{Th}}{R_2}\right)V_E}\]
En substituant ETh par son expression, puis par transformation de cette formule, on obtient:
\[\mathsf{\frac{V_S}{V_E}=-\frac{R_2}{R_1}\left(1+\frac{R_3}{R_2}+\frac{R_3}{R_4}\right)}\]
Le montage précédent peut aussi être proposé en version non inverseur:
Montage 2: ampli non inverseur:
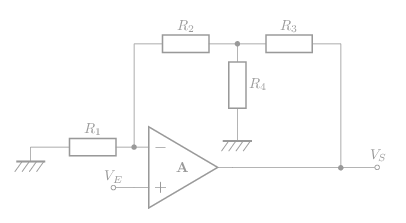
L'amplification:
\[\bbox[5px, border:1px solid]{\mathsf{\frac{V_S}{V_E}=\left( 1+\frac{R_2}{R_1}\right)\left(1+\frac{R_3}{R_4}+\frac{R_3}{R_1+R_2} \right)}}\]
La méthode de calcul reste la même, que celle du montage inverseur.
Le courant qui circule à travers R2 et R1, peut s'écrire de trois manières différentes:
\[\mathsf{\frac{V_{e-}}{R_1}=\frac{V_A-V_{e-}}{R_2}=\frac{V_A}{(R_1+R_2)}}\]
\[\mathsf{\implies\;V_A =\left(1+\frac{R_2}{R_1} \right)V_{e-}}\tag{3-3}\label{3-3}\]
Lois de Kirchoff au point A:
\[\mathsf{I_S=I_2+I_4}\]
Cela se traduit par:
\[\mathsf{\frac{V_S-V_A}{R_3}=\frac{V_A}{R_1+R_2}+\frac{V_A}{R_4}}\]
En isolant tous termes contenant VA, on obtient:
\[\mathsf{V_S=\left(1+\frac{R_3}{R_4}+\frac{R_3}{R_1+R_2}\right)V_A}\tag{3-4}\label{3-4}\]
Il suffit de substituer l'expression de VA (3-3) dans la formule précédente (3-4) pour avoir:
\[\mathsf{V_S=\left(1+\frac{R_2}{R_1}\right)\left(1+\frac{R_3}{R_4}+\frac{R_3}{R_1+R_2} \right)V_{e-}}\]
L'ampli op est idéal: Ve- = VE. Donc:
\[\mathsf{\frac{V_S}{V_E}=\left( 1+\frac{R_2}{R_1}\right)\left(1+\frac{R_3}{R_4}+\frac{R_3}{R_1+R_2} \right)}\]
Exemple d'application numérique pour ces deux montages:
R1 = 2,2kΩ; R2 =22kΩ; R3=10kΩ; R4=1kΩ.
Montage inverseur:
\[\mathsf{\frac{V_S}{V_E}=-\frac{22}{2.2}\left(1+\frac{10}{22}+\frac{10}{1}\right)=-114,5}\]
Montage non inverseur:
\[\mathsf{\frac{V_S}{V_E}=\left( 1+\frac{22}{2.2}\right)\left(1+\frac{10}{1}+\frac{10}{24.2} \right)=125.5}\]
Ces deux montages permettent d'obtenir un gain élevé, lorsqu'on a pas à disposition des résistances de très fortes valeurs. Car l'utilisation de très grandes résistances réduit l'intensité du courant à travers un circuit, et dans ces conditions les hypothèses des conditions idéales de l'ampli op pourraient être fausses.

