Autres types de montages:
Montage intégrateur:

La tension de sortie:
\[\bbox[5px, border:1px solid]{\mathsf{V_S=-\frac{1}{RC}\int{V_E}dt}}\]
Le courant qui circule à travers la résistance est le même que celui qui circule à travers le condensateur (ampli op idéal).
\[\mathsf{V_E=RI\;et\; V_S = - V_C}\]
Le courant I à travers le condensateur est égal à :
\[\mathsf{\frac{dq}{dt}\;sachant\; que,\; q=CV_C\;donc\; I=C\frac{dV_C}{dt}}\]
ainsi:
\[\mathsf{V_E=RC\frac{dV_C}{dt}= -RC\frac{dV_S}{dt}}\]
donc:
\[\mathsf{V_S=-\frac{1}{RC}\int{V_E}dt}\]
Montage dérivateur:

La tension de sortie:
\[\bbox[5px, border:1px solid]{\mathsf{V_S=-RC\frac{dV_E}{dt}}}\]
Les conditions sont les mêmes que pour le montage précédent.
\[\mathsf{V_E=V_C\;sachant\;que\;I = C\frac{dV_C}{dt}\;\;et\;\;V_S =-RI }\]
Donc:
\[\mathsf{V_S=-RC\frac{dV_E}{dt}}\]
Amplificateur logarithmique:
Le montage ci-dessous présente le principe d'un amplificateur logarithmique.

La tension de sortie:
\[\bbox[5px,border:1px solid]{\mathsf{V_S=-V_T\ell n\left(\frac{V_E}{RI_{ES}} \right)}}\]
VT: une constante qui dépend des paramètres du transistor;
IES: courant de saturation inverse de la jonction base-émetteur.
Avant tout calcul pour ce montage, il convient de voir d'abord quelques notions théoriques, qui amènent la caractéristique de la jonction émetteur-base d'un transistor bipolaire à correspondre à une loi de variation logarithmique.
Le courant collecteur IC d'un transistor bipolaire est donné par la relation:
\[\mathsf{I_C=\alpha I_E = \alpha I_{ES}\left[ e^{(q/kT)V_{BE}}-1\right]}\]
avec:
IC: courant collecteur;
IE: courant émetteur;
IES: courant de saturation inverse de la jonction base-émetteur;
k: constante de Boltzmann;
q: charge du proton;
T: température de la jonction en Kelvin;
VBE: tension base-émetteur.
On pose les hypothèses suivantes pour simplifier l'expression de IC:
\(\alpha = 1\); IES est très faible. Pour cela nous allons admettre que:
\[\mathsf{I_C=I_{ES}e^{(q/kT)V_{BE}}}\]
Posons VT=kT/q la valeur constante qui dépend du transistor. La formule devient:
\[\mathsf{I_C=I_{ES}e^{(V_{BE}/V_T)}}\tag{4-1}\label{4-1}\]
Calcul de VS en fonction de VE:
Le courant à travers la résistance est égal au courant IC (ampli op idéal):
\[\mathsf{V_E=RI_C}\]
Selon l'expression (4-1):
\[\mathsf{V_E=RI_{ES}e^{(V_{BE}/V_T)}}\tag{4-2}\label{4-2}\]
Sachant que :
\[\mathsf{V_S=-V_{BE}}\]
L'expression (4-2) devient:
\[\mathsf{V_E=RI_{ES}e^{(-V_S/V_T)}}\]
Par transformation de formule on a:
\[\mathsf{V_S=-V_T\ell n\left(\frac{V_E}{RI_{ES}} \right)}\]
Amplificateur exponentiel:
Le montage ci-dessous présente le principe d'un amplificateur exponentiel.

La tension de sortie:
\[\bbox[5px, border:1px solid]{\mathsf{V_S=RI_{ES}e^{(-V_E/V_T)}}}\]
VT: une constante qui dépend des paramètres du transistor;
IES: courant de saturation inverse de la jonction base-émetteur.
Bilan des tensions:
\[\mathsf{V_E=-V_{BE}}\]
\[\mathsf{V_S=RI_C}\]
Le courant:
\[\mathsf{I_C=I_{ES}e^{(V_{BE}/V_T)} = I_{ES}e^{(-V_E/V_T)}}\]
Donc:
\[\mathsf{V_S=RI_{ES}e^{(-V_E/V_T)}}\]
Les deux structures précédentes : l'amplificateur logarithmique et exponentiel, démontrent juste le principe de ces fonctions. Mais en pratique, elles présentent quelques défauts:
-
- Le défaut de stabilité,
- La dépendance de la structure vis à vis des variations de températures.
Dans les deux cas, ces défauts peuvent être compensés par l'ajout de composants additionnels.
Montages complexes:
1 - Multiplieur de tension:

On suppose que les quatre transistors sont identiques et de même température.
La tension de sortie:
\[\bbox[5px, border:1px solid]{\mathsf{V_S=\frac{V_1V_2}{V_3}}}\]
Ce résultat n'est valable que si V1, V2 et V3 sont des tensions positives.
Pour calculer VS, considérons d'abord le sous-ensemble suivant:
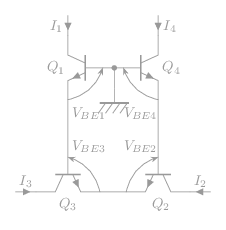
Bilan des tensions:
\[\mathsf{V_{BE_1}+V_{BE_3}-V_{BE_2}-V_{BE_4}=0}\]
on peut alors écrire:
\[\mathsf{V_{BE_1}+V_{BE_3}=V_{BE_2}+V_{BE_4}}\tag{5-1}\label{5-1}\]
Pour les différents courants:
\[\mathsf{I_1\text{ : courant collecteur de Q1: }I_1=I_{ES}e^{(V_{BE_1}/V_T)}}\]
\[\mathsf{I_2\text{ : courant collecteur de Q2: }I_2=I_{ES}e^{(V_{BE_2}/V_T)}}\]
\[\mathsf{I_3\text{ : courant collecteur de Q3: }I_3=I_{ES}e^{(V_{BE_3}/V_T)}}\]
\[\mathsf{I_4\text{ : courant collecteur de Q4: }I_4=I_{ES}e^{(V_{BE_4}/V_T)}}\]
On en déduit:
\[\mathsf{V_{BE_1}=V_T\ell n\left(\frac{I_1}{I_{ES}} \right)}\]
\[\mathsf{V_{BE_2}=V_T\ell n\left(\frac{I_2}{I_{ES}} \right)}\]
\[\mathsf{V_{BE_3}=V_T\ell n\left(\frac{I_3}{I_{ES}} \right)}\]
\[\mathsf{V_{BE_4}=V_T\ell n\left(\frac{I_4}{I_{ES}} \right)}\]
A partir de l'expression (5-1):
\[\mathsf{V_T\ell n\left(\frac{I_1I_3}{I_{ES}^2} \right)=V_T\ell n\left(\frac{I_2I_4}{I_{ES}^2} \right)}\]
On peut écrire:
\[\mathsf{I_1I_3=I_2I_4}\tag{5-2}\label{5-2}\]
Bilan des courants par ampli op:
\[\mathsf{\text{A1 : }I_1=\frac{V_1}{R}+\frac{V_3}{R}}\]
\[\mathsf{\text{A3 : }I_3=\frac{V_2}{R}+\frac{V_3}{R}}\]
\[\mathsf{\text{A4 : }I_4=\frac{V_3}{R}}\]
\[\mathsf{\text{A2 : }I_2=\frac{V_1}{R}+\frac{V_2}{R}+\frac{V_3}{R}+\frac{V_S}{R}}\]
En substituant ces courant dans l'expression (5-2) et en simplifiant on obtient:
\[\mathsf{V_1V_2=V_SV_3\;soit\;V_S=\frac{V_1V_2}{V_3}}\]
2 - Montage redresseur:

Ce montage permet de redresser sur une seule alternance un signal d'entrée VE sinusoïdal.
Lorsque VE > 0, la diode D1 conduit et D2 est bloquée. V1 = 0 et V2 = -VE;
Lorsque VE < 0, la diode D1 est bloquée et D2 conduit. V1 = -VE. Etant dans l'alternance négative de VE, on a une valeur positive; V1 = |VE|.
Pour obtenir un redresseur double alternance, Il faudra rajouter un ampli op supplémentaire puis utiliser les deux signaux V1 et V2.
3 - Exemple de mise en oeuvre: convertisseur RMS:
La figure ci-après propose un montage théorique plus détaillé, qui permet de calculer la valeur efficace d'un signal périodique: cas d'un signal sinusoïdal:

La tension de sortie :
\[\bbox[5px, border:1px solid]{\mathsf{V_S=\sqrt{\frac{1}{T}\int_{0}^T |V_E(t)|^2dt}}}\]
L'amplificateur A1 est un redresseur de tension. Lorsque VE > 0, la diode et bloquée, et V1=0. Le courant IC1 du transistor Q1 est égal à la somme des courants issus de V1 et de VE. Ce courant est proportionnel à la tension d'entrée redressée. La tension de sortie de l'amplificateur A2, est proportionnelle à ln|VE(t)|2. Et le courant collecteur IC2 su transistor Q2, est proportionnel au rapport VE(t)2/VS.
La présence du condensateur C transforme en valeur moyenne le courant IC2, puis en sortie de A3 fournit une tension VS égale à la valeur efficace de VE(t).
On va s'intéresser à l'amplificateur A2, et aux composants qui l'entourent (R, R/2, Q1, Q3) et plus loin au comportement de la diode D2:
Transistor Q1:
Le courant collecteur du transistor Q1
\[\mathsf{I_{C1}=\frac{V_E}{R}+\frac{V_1}{R/2}=\frac{V_E}{R}+\frac{2V_1}{R}=\frac{V_E+2V_1}{R}}\]
A présent le terme VE + 2V2:
Lorsque VE > 0, D2 est bloquée. V2 = 0.
\[\mathsf{\implies \quad I_{C1}=\frac{V_E}{R}}\]
Lorsque VE < 0, D2 conduit; et V2 = -VE. Etant dans l'alternance négative de VE, donc V2 = VE.
\[\mathsf{\implies\quad I_{C1}=\frac{-V_E+2V_E}{R}=\frac{V_E}{R}}\]
Dans tous les cas:
\[\mathsf{I_{C1}=\frac{|V_E|}{R}}\]
Le courant collecteur de Q1 a aussi avoir pour expression:
\[\mathsf{I_{C1}=I_{ES}e^{V_{BE}/V_T}}\]
On peut donc écrire:
\[\mathsf{\frac{|V_E|}{R}=I_{ES}e^{V_{BE}/V_T}}\tag{6-1}\label{6-1}\]
D'autre part en tenant compte de l'autre transistor monté en série:
\[\mathsf{V_A=-2V_{BE}\;\implies\;V_{BE}=\frac{-V_A}{2}}\]
L'expression (6-1) devient:
\[\mathsf{\frac{|V_E|}{R}=I_{ES}e^{-V_A/2V_T}}\]
Par transformation de formules:
\[\mathsf{V_A=-V_T\ell n\frac{|V_E|^2}{(RI_{ES})^2}}\]
Transistor Q3:
Le courant collecteur:
\[\mathsf{I_{C3}=I_{ES}e^{(V_{BE}/V_T)}=I_{ES}e^{(-V_B/V_T)}}\]
\[\mathsf{V_S=RI_{C3}=RI_{ES}e^{(-V_B/V_T)}}\]
Par transformation:
\[\mathsf{V_B=-V_T\ell n\frac{V_S}{RI_{ES}}}\]
Transistor Q2:
La tension au point B:
\[\mathsf{V_B = V_A+V_{BE}}\tag{6-2}\label{6-2}\]
Selon l'expression (6-2):
\[\mathsf{V_{BE} = V_B -V_A=-V_T\ell n\frac{V_S}{RI_{ES}}+V_T\ell n\frac{|V_E|^2}{(RI_{ES})^2}}\]
\[\mathsf{V_{BE}=V_T\ell n\left(\frac{|V_E|^2}{V_SRI_{ES}} \right)}\tag{6-3}\label{6-3}\]
A partir de VBE en (6-3), l'expression de la tension de sortie:
\[\mathsf{V_S= RI_{C2}=RI_{ES}e^{(\ell n|V_E|^2/V_SRI_{ES})}}\]
En simplifiant:
\[\mathsf{V_S^2=|V_E|^2}\]
La présence du condensateur C donne une valeur moyenne à la sortie de A3:
\[\mathsf{V_S^2=\frac{1}{T}\int_{0}^T |V_E(t)|^2dt}\]
soit:
\[\mathsf{V_S=\sqrt{\frac{1}{T}\int_{0}^T |V_E(t)|^2dt}}\]
En pratique, un des principes pour obtenir une valeur efficace vraie d'un signal est donné par la figure ci-après:

Exemple de réalisation industrielle: AD536 fabriqué par Analog Devices.

