Oscillateurs à amplificateur opérationnel

Lorsqu’il fonctionne en régime d'instabilité, un amplificateur opérationnel peut se transformer en oscillateur. Dans ces conditions, il est capable, de produire un signal périodique.

Parmi les types d’ondes possibles que peut produire un amplificateur opérationnel, il y a des formes sinusoïdales, rectangulaires, triangulaires ou quelconques. Il existe un grand nombre d’oscillateurs sinusoïdaux nous n'allons en présenter que trois, puis nous finirons par un oscillateur rectangulaire.

Oscillateurs sinusoïdaux :

D’une façon générale, un système bouclé se présente sous la forme suivante:

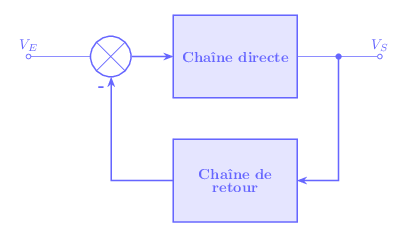
Si V_S représente la tension de sortie, V_e la tension d'entrée de la chaîne directe, et V_R la tension de sortie de la chaîne de retour, on note:

Le gain de la chaîne directe

\[\mathsf{A = \frac{V_S}{V_e}}\]

Le gain de la chaîne de retour

\[\mathsf{B = \frac{V_R}{V_S}}\]

La chaîne de retour est généralement constituée de composants passifs; dans le cas particulier d'un régime sinusoïdal, on notera plutôt B(j\(\omega\)).

La fonction de transfert

\[\mathsf{\frac{V_S}{V_E}=\frac{A}{1+AB(j\omega)}}\]

Une condition possible pour que le montage oscille quand V_E = 0, revient à vérifer 1 + AB(j\(\omega\)) = 0, soit AB(j\(\omega\)) = -1. Il faut pour cela que |AB(j\(\omega\))| soit au moins égal à 1.

Quelques exemples d’oscillateurs sinusoïdaux :

Oscillateur à pont de Wien :

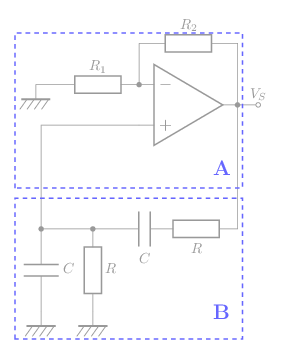
Les composants de ce montage génèrent un « bruit », suffisant pour faire démarrer les oscillations. L'amplitude de la sinusoïde générée augmente, puis se stabilise à cause de la saturation de l’amplificateur opérationnel.

Amplification:

Chaîne directe :

\[\mathsf{A=1+\frac{R_2}{R_1}}\]

Chaîne de retour: 

\[\mathsf{B(j\omega)=\frac{1}{3+j\left(RC\omega-\frac{1}{RC\omega}\right)}}\]

Si nous traduisons la condition |AB| = 1, on annule la partie imaginaire du résultat; nous obtenons:

\[\mathsf{f_0=\frac{1}{2\pi RC}}\]

\[\mathsf{f_0:\text{fréquence des oscillations}}\] 

La chaîne directe devra avoir une amplification minimale:

A = 1 + R₂/R₁ = 3, \(\implies\) la valeur minimale de R₂ = 2R₁.

Oscillateur à réseau déphaseur:

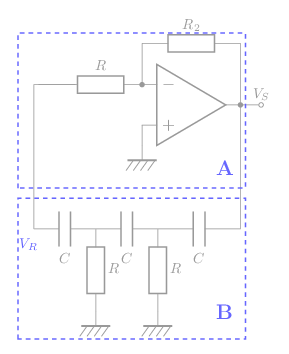
Amplification:

Chaîne directe :

\[\mathsf{A=-\frac{R_2}{R}}\]

Chaîne de retour:

\[\mathsf{B(j\omega)=\frac{1}{1+\large{\frac{6}{jRC\omega}+\frac{5}{(jRC\omega)^2}+\frac{1}{(jRC\omega)^3}}}}\]

La fréquence des oscillations : \(\mathsf{f_0=1/2\pi RC\sqrt{6}}\).

La condition d'amplification minimale: \(\mathsf{R_2/R=29}\).

Oscillateur  Colpitts:

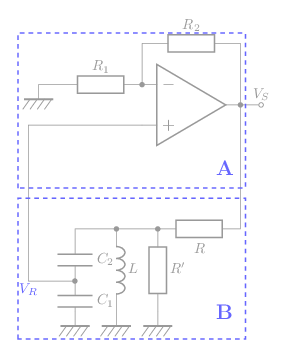
Amplification :

Chaîne directe :

\[\mathsf{A =\frac{V_S}{V_R}=1+\frac{R_2}{R_1}}\]

Chaîne de retour :

\[\mathsf{B(j\omega)=\frac{V_R}{V_S}=\frac{1}{\left(1+\frac{C_1}{C_2}\right)\left[\left(1+\frac{R}{R’}\right)+j\left(C\omega-\frac{1}{L\omega}\right)\right]}}\]

Avec C capacité équivalente des condensateurs C₁ et C₂ montés en série.

\[\mathsf{C=\frac{C_1C_2}{(C_1+C_2)}}\]

Le produit AB(j\(\omega\)) :

\[\mathsf{\frac{\left(1+\frac{R_2}{R_1}\right)}{\left(1+\frac{C_1}{C_2}\right)\left[\left(1+\frac{R}{R’}\right)+j\left(C\omega-\frac{1}{L\omega}\right)\right]}}\]

Permet de traduire les conditions d’oscillations |AB(j\(\omega\))| = 1, par :

L’annulation de la partie imaginaire  \(\implies\) LC\(\omega ^2\)=1 \(\implies \;\omega=\frac{1}{\sqrt{LC}}\)

Soit une fréquence d’oscillation :

\[\mathsf{f_0=\frac{1}{2\pi\sqrt{L\left(\frac{C_1C_2}{C_1+C_2}\right)}}}\]

Et la condition sur l’amplification :

\[\mathsf{1+\frac{R_2}{R_1}=\left(1+\frac{C_1}{C_2}\right)\left(1+\frac{R}{R’}\right)}\]

Un oscillateur Colpitts est souvent utilisé pour produire des signaux hautes fréquences.  L’emploi d’un amplificateur opérationnel n’est pas  adapté à cet effet, le transistor s'avère être un bon compromis dans ce cas.

On démontre par une approche théorique en prenant un modèle du transistor en petits signaux que l'on retrouve une fréquence d’oscillation de la forme:

\[\mathsf{f_0=\frac{1}{2\pi\sqrt{L\left(\frac{C_1C_2}{C_1+C_2}\right)}}}\]

Et la condition sur l’amplification dépend des paramètres internes du transistor.

A partir du schéma précédent, il est possible d'obtenir un oscillateur Hartley, il suffit pour cela de remplacer dans la cellule L - C₁ - C₂, par une cellule du type C - L₁ - L₂, en substituant  L par C, puis C₁ et C₂ par L₁ et L₂ respectivement.

Oscillateur à signaux rectangulaire:

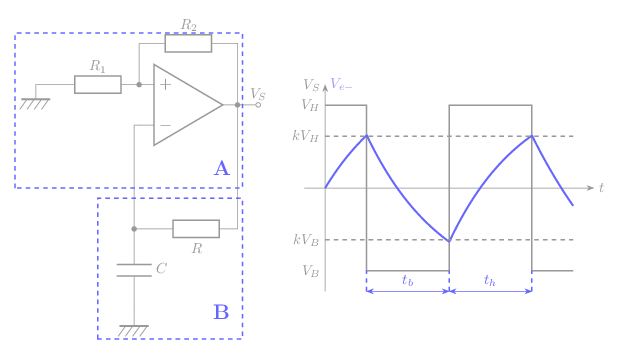
L’effet du réseau R₁ – R₂ sur l’entrée e+, est plus rapide que celui du réseau R- C sur l’entrée e-, au départ.

Posons les niveaux de tension de saturation en sortie de l’ampli. Op à l’état haut et bas : +Vsat = V_H et –Vsat=V_B

Supposons le condensateur initialement déchargé. Donc V_e-=0, et la sortie de l’ampli. Op bascule à V_H. Le courant est positif et le condensateur charge à travers la résistance R, la tension aux bornes du condensateur augmente jusqu’à atteindre le seuil de tension V_e+ (kV_H).

L’ampli. Op fait basculer sa sortie à V_B. Le courant change de sens, puis le condensateur se décharge à travers la résistance, la tension aux bornes du condensateur décroît jusqu’à V_e- (kV_B). La sortie de l’ampli. Op bascule de nouveau vers V_H, le condensateur recommence sa charge à travers R, puis le cycle des oscillations est entretenu.

La fréquence d’oscillations :

\[\mathsf{f_0=2\tau\ell n\left(\frac{1+k}{1-k}\right)}\]

Avec \(\tau=RC\) et k = R₁/(R₁+R₂).

De nombreux montages oscillateurs à base d’amplificateurs opérationnels sont possibles. Mieux encore, des circuits spécialisés existent sur marché pour assurer cette tâche, on peut citer par exemple l'un des plus populaires de sa génération le 555 (NE555, LM555,...).